Load Balancing Techniques

In this blog, you will learn about different ways a load balancer manages to send requests among servers in a distributed system. Let’s start with no noise.

Round Robin

As the name suggests, in this algorithm the load balancer keeps assigning new requests to the next available server. Suppose we have 5 servers registered with our load balancer and a pointer that points to the current server to be assigned, called current_server:

Servers:  [s0, s1, s2, s3, s4]

and 10 requests are coming:

Requests: [r0, r1, r2, r3, r4, r5, r6, r7, r8, r9]

The load balancer keeps accepting requests, assigns each request to current_server, and then increments it as:

current_server = (current_server + 1) % N

This way, current_server will point to s0 again after assigning a request to s4.

This is one of the simplest algorithms to design a load balancer. But it has a big problem:

• It assumes all servers are equal, which is often false.
  For example, s2 could be a lightweight machine, whereas s3 could be a machine with much more processing power.

To avoid this problem, we can use Weighted Round Robin, where more powerful servers get more chances by appearing multiple times in the server list, like this:

Servers: [s0, s0, s0, s1, s2, s2, s2, s3, s4]

In the above example, s0 and s2 will receive more requests than usual, as they appear more times in the array.

However, in this algorithm, there is no request–server relationship maintained. What I mean is that servers often store some data in their cache to serve a particular type of request quickly, but for this to work, the load balancer must ensure that those requests always reach the same server.

In Round Robin, no such relationship is maintained between a request and a server. So, we need a different way to solve this problem. This is where Hashing comes in.

Hashing

Let’s start directly with an example where we have:

• N (number of servers) = 4
• A hash function that takes some parameter from the request and hashes it
• We take the modulo of the hash result so that the value ranges between 0 and N-1

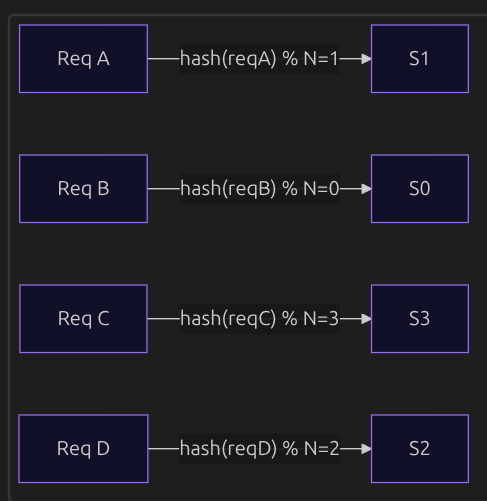
Note: Load balancer uses some property of the request to hash it, like userID and this userID can be used by the server as a cache key to store the data related to this user.

Since the hash function is deterministic, it will always produce the same result for a given input. So ReqA will always go to S1, and any cache stored for this request at S1 will be reused to serve future requests. This solves the cache-locality problem of Round Robin.

But what if we want to add a new server, or if a server goes down?

That’s a fair question. As you can see from the formula hash(req) % N, the result depends on N. This means that if we add a new server, a reshuffling of requests will occur, impacting all servers.

What kind of impact?
As we know, servers keep cached data to serve requests efficiently. After reshuffling, servers may start receiving requests for which they do not have cached data, leading to a large number of cache misses and a noticeable performance impact.

Our goal is to minimize the cost of adding or removing servers from the system.

To solve this problem, we use Consistent Hashing, which brings us to the main topic of this blog.

Consistent Hashing

In consistent hashing, we hash the server IDs and place them on a ring based on their hash values, like this:

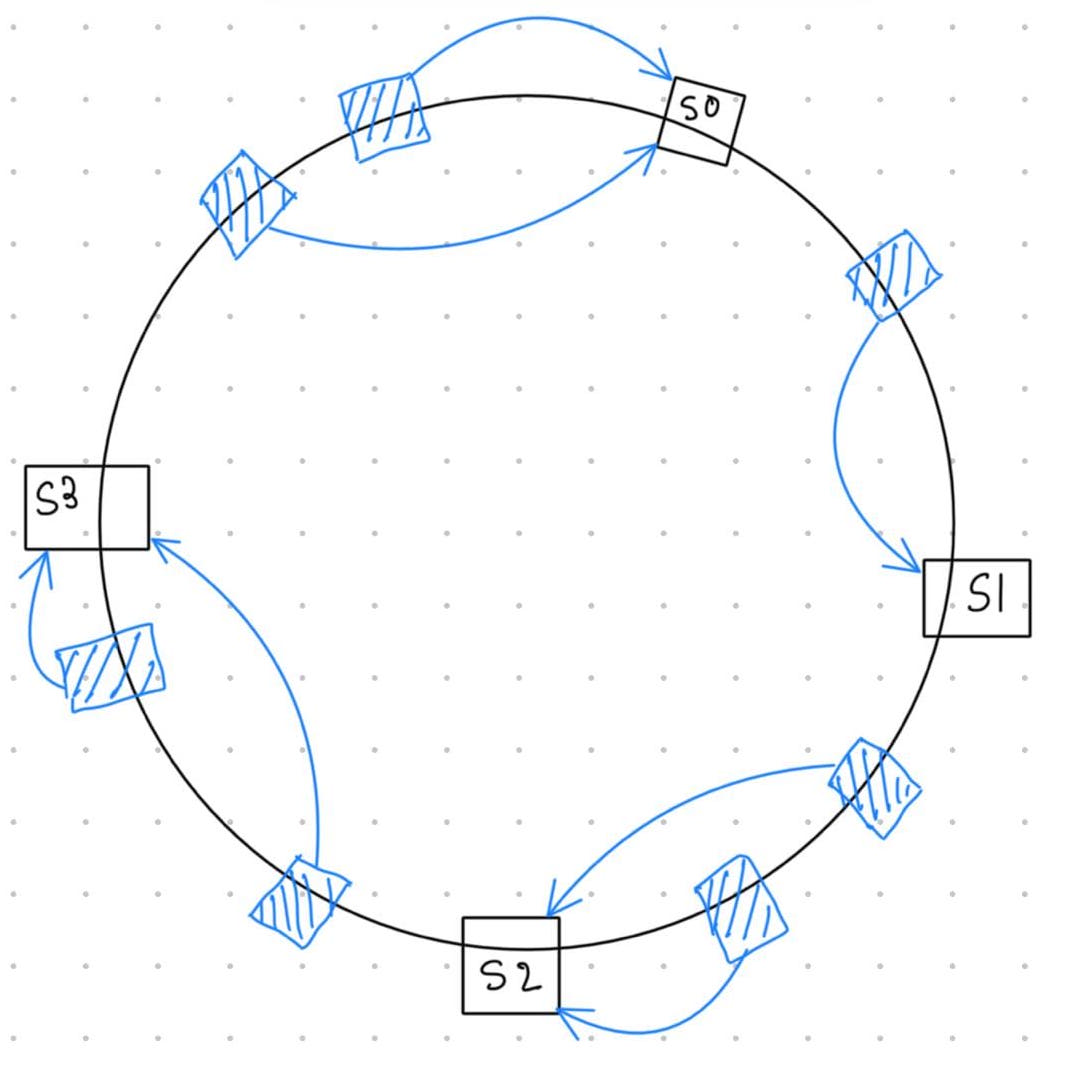
In the figure, blue boxes represent requests and black/red boxes represent servers.

First, look at the servers S0...S3 placed on the ring according to the values returned by the hash function. Next, we hash the requests (using some property from the request object) and place them on the same ring.

For each request, we move in the clockwise direction on the ring, and the first server encountered is responsible for serving that request.

Now let’s see how this approach solves the problem of adding new servers.

Look at this figure:

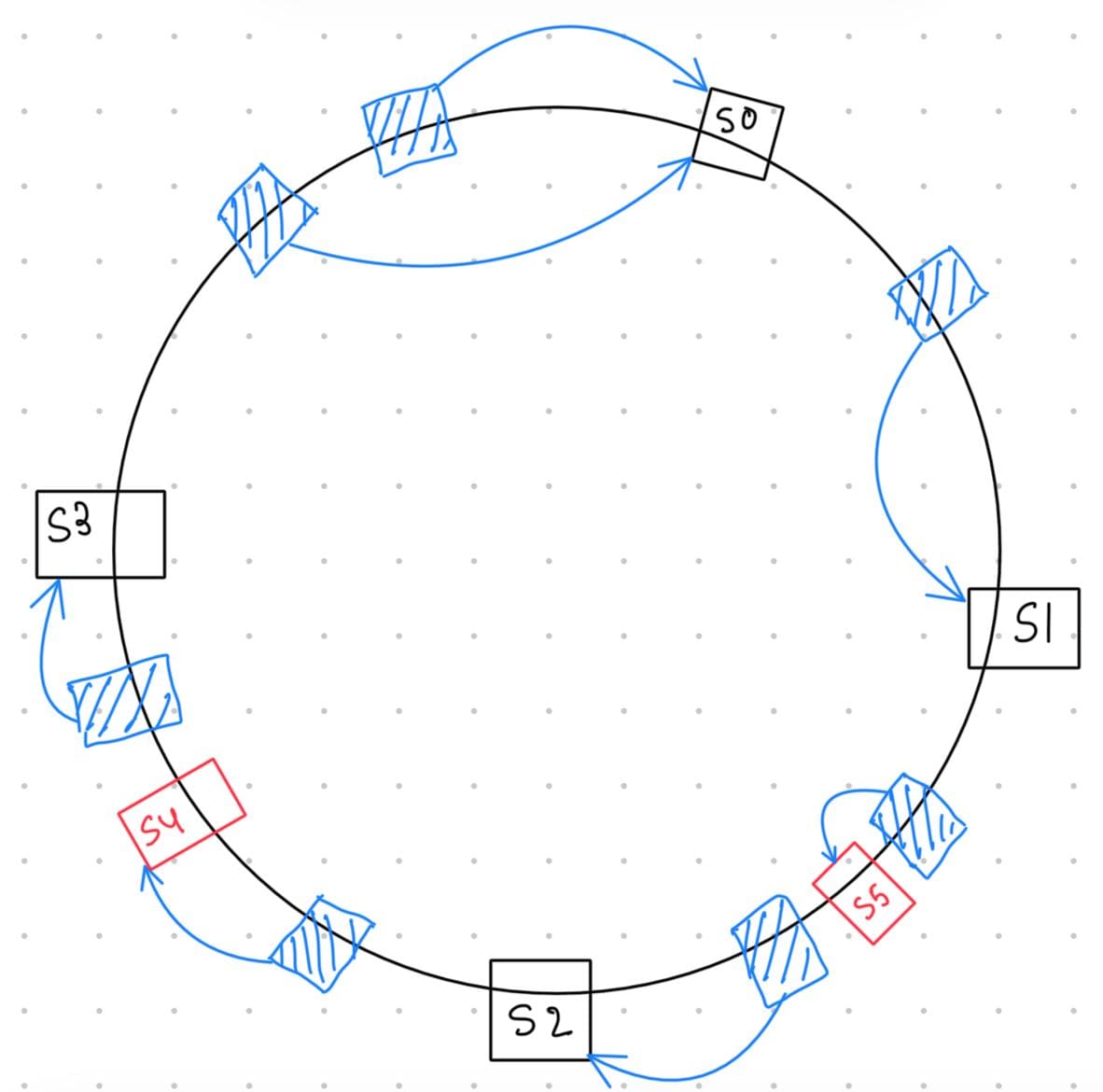
Here, S4 and S5 are newly added servers. Due to their addition, only S2 and S3 are affected — unlike the normal hashing approach, where all servers are impacted.

• The load on S2 is reduced due to the addition of S5
• The load on S3 is reduced due to the addition of S4

The principal advantage of consistent hashing is that the arrival or departure of a node only affects its immediate neighbors, while other nodes remain unaffected.

So you just learnt one of the most important topic when it comes to load balancing, that is "Consistent Hashing".

The basic consistent hashing algorithm presents some challenges:

• The random position assignment of each node on the ring leads to non-uniform data and load distribution.
• The basic algorithm is oblivious to the heterogeneity in the performance of nodes.

This blog would become too long if I discussed how to address these challenges here. Stay tuned for the next blog, where I’ll explain how large-scale systems modify the basic algorithm to overcome these limitations.

- Piyush